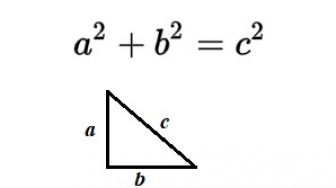Suara.com - Rumus bangun ruang merupakan salah satu materi pelajaran matematika yang harus dipahami. Bangun ruang merupakan bangun tiga dimensi yang memiliki ruang dan dibatasi oleh sisi-sisinya. Bangun ruang memiliki volume, isi, dan tiga komponen, yaitu sisi, rusuk, dan titik sudut. Terdapat rumus-rumus bangun ruang yang dibagi menjadi dua macam, yakni bangun ruang sisi datar dan lengkung.
Bangun ruang sisi datar merupakan bangun tiga dimensi yang memiliki sisi berbentuk datar. Bangun ruang sisi lengkung merupakan bangun tiga dimensi dengan bagian sisi berbentuk melengkung. Kategori bangun ruang sisi datar, meliputi kubus, balok, prisma segitiga, dan limas. Sementara itu, yang termasuk dalam bangun ruang sisi lengkung, yakni tabung, kerucut, dan bola.
Dilansir dari berbagai sumber, berikut rumus bangun ruang dan contoh soalnya.
1. Rumus Bangun Ruang Kubus
Bangun ruang kubus memiliki 6 sisi, 12 rusuk, dan 8 titik sudut.
- Luas Kubus
Rumus Luas Kubus, yaitu: L = 6 x s - Keliling Kubus
K = 12 x s - Volume Kubus
Rumus volume kubus, yaitu: V = s x s x s (s3)
L adalah luas, V merupakan volume, s yaitu sisi.
Contoh soal rumus kubus:
Soal: Sebuah kotak kapur memiliki sisi 10 cm, berapa luas, keliling, dan volumenya?
Jawab:
L = 6 x s = 6 x 10 = 60 cm2.
Baca Juga: Rumus Trapesium Lengkap dengan Jenis dan Ciri-cirinya
K = 12 x s = 12 x 10 = 120 cm.
V = s x s x s = 10 x 10 x 10 = 1000 cm3.
2. Rumus Bangun Ruang Balok
Balok merupakan bangun ruang yang terdiri atas 6 sisi, 12 rusuk, dan 8 titik sudut.
- Luas balok, yaitu: L = 2 x [(p x l) + (p x t) + (l x t)]
- Keliling balok = K = 4 x (p + l + t)
- Volume balok, yaitu: V = p x l x t
P merupakan panjang, l adalah lebar, K sama dengan keliling, dan t yaitu tinggi.
Contoh soal rumus balok: